Question

What is the last term of a geometric progression whose sum is 31/64, its first tem is 1/4 and rhe ratio 1/2 ?

Answer 1

The first term is a = 1/4

The common ratio is d = 1/2.

The sum of geometric progression is S = 31/64.

The formula for the geometric progression is,

`S=(a(1-r^n))/(1-r)`

Substitute the given values in the expression to obtain the value of n.

`\begin{gathered} (31)/(64)=((1)/(4)(1-((1)/(2))^n))/(1-(1)/(2)) \\ (31)/(64)=(1)/(2)(1-(1)/(2^n)) \\ (1)/(2^n)=1-(31)/(32) \\ 2^n=(32)/(32-31) \\ 2^n=2^5 \\ n=5 \end{gathered}`

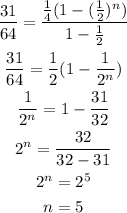
The nub er of terms is n = 5.

The last term of geometric progression is,

`a_n=ar^(n-1)`

Substitute the values in the equation to obtain the last term of series.

`\begin{gathered} a_5=(1)/(4)((1)/(2))^(5-1) \\ =(1)/(4)\cdot(1)/(16) \\ =(1)/(64) \end{gathered}`

So last term of geometric progression is 1/64.