Question

a long-distance swimmer crosses a lake swimming 6 mi in one and a half hours with the current on the way back to swimmer cannot move forward at all because of going against the current eventually the swimmer gives up and waits for a ride back home as soon assume the swimmer swims at a constant speed and assume the current is also at a constant speed what is the speed of the current

Answer 1

We know that, when the swimmer swims with the current, he cross the 6 miles in 1.5 hours.

When the swimmer tries to swim against the current, the displacement is zero.

We can conclude two things:

- The resulting speed when he goes with the current is the speed of the swimming plus the speed ot the current.

- When he swims against the current, he can not move forward because the speed of swimming equals the speed of the current.

Then, we can write:

`v_c+v_s=v=(\Delta x)/(\Delta t)=\frac{6\text{ miles}}{1.5\text{ hours}}_{}=4\text{ miles/hour}`

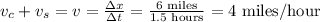
vc: speed of the current, vs: speed of the swimming

`\begin{gathered} v_c=v_s=4-v_c \\ 2v_c=4 \\ v_c=v_s=(4)/(2)=2\text{ miles/hour} \end{gathered}`

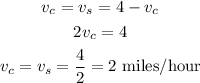
As both speeds are equal, the speed of the current and the speed of the swimming are half the speed of the average speed when swimming with the current.

Answer:

The speed of the current is 2 miles per hour.