Question

The volume of Figure B is three times the volume of Figure A.5xA. TrueA6O B. False

Answer 1

SOLUTION;

Case: Comparing Volumes

Given:

A Square-based pyramid and a cylinder

Required: show that the Volume of figure B is 3 times that of figure A

Method:

Step 1: Find we find the Volume of the square-based pyramid.

Volume

`\begin{gathered} V=(1)/(3)l* w* h \\ V=(1)/(3)*5\pi*5\pi*6\pi \\ V=50\pi^3 \end{gathered}`

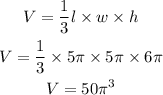
Step 2: Find we find the Volume of the Cylinder

`\begin{gathered} V=\pi r^2h \\ V=\pi*(5\pi)^2*6 \\ V=\pi*5\pi*5\pi*6 \\ V=150\pi^3 \end{gathered}`

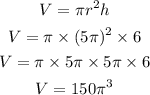
Step 3:

Dividing the volumes to check if it gives 3

`\begin{gathered} ratio=(V_B)/(V_A) \\ ratio=(150\pi^3)/(25\pi^3) \\ ratio=3 \end{gathered}`

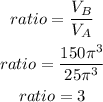
Step 4: Since the ratio of the volumes of figure B to A is 3, it means that voume figures B is three times the Volume of figure A.