Question

need help with this and I need practice with the 'ac' method so please use the 'ac' method like it says

Answer 1

To factor the given expression using the AC method, here are the steps:

Before proceeding to the steps, make sure to arrange the terms first according to their degree. Since the expression is already arranged from greatest to no degree, we can proceed with the steps.

1. Multiply the numerical coefficients of the first term and the constant term.

`6*-12=-72`

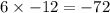
2. Locate the numerical coefficients of the middle term. The coefficient is -34.

3. Find any factors of -72 that would sum to -34.

Let's list down the factor of -72 and add them.

1 and -72 → -71

2 and -36 → -34

As we can see, the factors of -72 that add up to -34 are 2 and -36.

4. Rewrite the given expression by rewriting the middle term into (2u - 36u).

`6u^2-34u-12\Rightarrow6u^2+2u-36u-12`

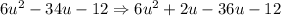
5. Separate the 4 terms into groups of two.

`(6u^2+2u)-(36u+12)_{}`

6. Factor each group by their common factor.

`2u(3u+1)-12(3u+1)`

7. As we can see in step 6, both groups have the same common factor that is (3u + 1), hence, we can rewrite it as:

`(2u-12)(3u+1)_{}`

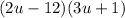
Therefore, the given expression can be factored to (2u - 12)(3u + 1) as shown above.

To factor this further, we can also factor 2u - 12 into 2(u - 6). Hence, the other factor for the expression is:

`2(u-6)(3u+1)`