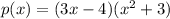Polynomial Factoring
Factor the following polynomial:
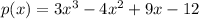
Let's group the first two and the last two terms:
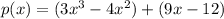
Factoring out x^2 from the first two terms and 3 from the last two terms
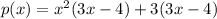
Note the expression 3x-4 is common to both groups. Factoring it out:
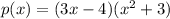
The second factor is a sum of squares, so it cannot be factored further. The final factorization is: