When we have the statement " y varies inversely as x ". We have the next equation:

Where k represents the constant between them.
Replace using the given values:
y=2
x=8
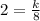
Now, solve for k:
Multiply both sides by 8
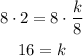
Hence, the constant value k is equal to 16.
Let's find x where y=14 and k =16.
Use the same equation to find x and replace it with the given values:
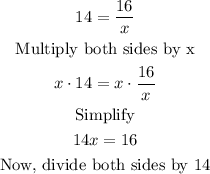
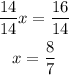
Hence, when y=14, the x value will be 8/7