Since Lauren has a half-hour head start, let's calculate the distance covered in this time:
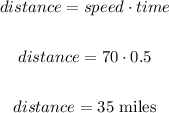
Since they are driving in opposite directions, the relative speed is the sum of speeds.
So, to find when the distance between then will be 340 miles, we can use the same formula, but now considering the initial position:

If we add the half-hour head start, the total time is 2.76 hours.