We are given the following binomial probability distribution
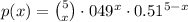
Recall that the general form of the binomial probability distribution is given by

Comparing the given binomial probability distribution with the general form,
The probability of success is p = 0.49
The sample size is n = 5
Let us find the probability for x = 0, 1, 2, 3, 4, 5
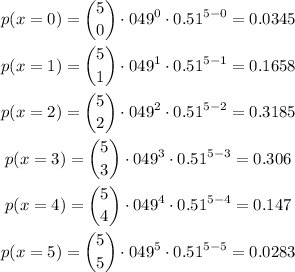
Now compare the above probabilities with the given graphs.
Notice that the above probabilities exactly matches with graph A
Therefore, the correct answer is graph A.
(b) Mean and standard deviation:
Recall that the mean of the binomial probability distribution is given by
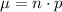
Where n is the sample size and p is the probability of success
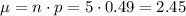
Therefore, the mean is 2.45
Recall that the standard deviation of the binomial probability distribution is given by
![\begin{gathered} \sigma=\sqrt[]{n\cdot p\cdot(1-p)} \\ \sigma=\sqrt[]{5\cdot0.49\cdot(1-0.49)} \\ \sigma=1.12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pcl2q8yf0jg9bnqe37mx9bwc9y0xox1rap.png)
Therefore, the standard deviation is 1.12
(c) The mean is 2.45 and the standard deviation is 1.12
We need to show two standard deviation interval below and above the mean.
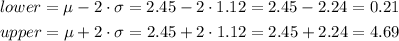
So, the two points are 0.21 and 4.69
As you can see, graph C shows these two points.