Question

Given the function (x) = 2x+7 what is the average rate of change over the interval 3

Answer 1

The average rate of change of a function is given by the following formula.

`r=(f(b)-f(a))/(b-a)`

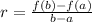
Where a = 3 and b= 11.

First, evaluate the function when x = 3.

`\begin{gathered} f(x)=2x+7_{} \\ f(3)=2(3)+7=6+7=13 \end{gathered}`

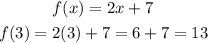
This means f(a) = 13.

Second, evaluate the function when x = 11.

`f(11)=2(11)+7=22+7=29`

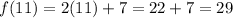
This means f(b) = 29.

Once we have all the values we need, we can find the average rate of change using the formula.

`\begin{gathered} r=(f(b)-f(a))/(b-a) \\ r=(29-13)/(11-3) \\ r=(16)/(8) \\ r=2 \end{gathered}`

Therefore, the average rate of change is 2.