Hello there. To solve this question, we'll have to remember some properties about slopes of a terminal ray.
Given that the initial ray of an angle it pointing in 12 o'clock direction and turns counterclockwise, when θ is the measure of the varying angle in radians, we have to determine:
The slope of the terminal ray, if θ = 0.8
Write an expression (in terms of θ) that represents the varying slope of the terminal ray.
We start drawing the diagram. With a circle with radius R, we make:
The slope of the terminal ray can be determined by taking the tangent of the angle, but don't forget this angle starts after 90º.
Therefore the slope might be:
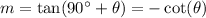
This is also the expression for the varying slope of the terminal ray, in terms of θ.
To find the slope when θ = 0.8, simply plug it, in radians, and use a calculator to evaluate the expression:
