Answer:
Step-by-step explanation:
a) Here, we want to calculate the length of the sides of the triangle ABC
Firstly, we need to get the coordinates of the points
A (-7,-3)
B(-8,3)
C (-5,3)
To find the length of any of the sides, we use the distance between points formula
That would be:
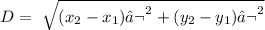
For BC, we have:
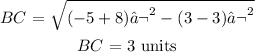
For AC, we have:
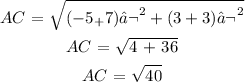
b) Here, we want to calculate the area of triangle ABC.
We can use Heron's formula here: