Question

Which of the relationships below represents a function with a lesser rate of change (slope) than the function y= -3/4x + 2?

Answer 1

To determine which of the relationships represents a function with a lesser rate of change than the given function, we need to determine the rate of change for this function, then we will compare with the rate of change calculated from each of the presented ones.

A generic equation of a line in the slope-intercept form is given by:

`y=ax+b`

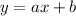
where a stands for the slope. From this, we are able to determine that the slope from the given equation is (-3/4). Because we want an equation with a lesser rate of change, we need it with the absolute value of the slope lower than the absolute value of the given equation. In the given equation, the absolute value of the slope is (3/4) (positive).

Now, to determine the slope of each of the given relationships, we will use the following method to calculate the slope:

`a=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)`

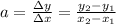
where x1, y1, x2, and y2 stand for the values of any points in the set of values given.

Now, let's calculate for each one:

A)

Let us use the points (0, 4) and (4, 1), that are easy to see in the graph:

`a_A=(1-4)/(4-0)=-(3)/(4)`

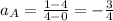
This is just equal to the one provided by the problem, and for this reason, it is not the correct answer.

B)

Among the given values we can pick any pair. Let us choose (1, -3) and (4, 3). Now we calculate:

`a_B=(3-(-3))/(4-1)=(6)/(3)=2`

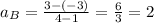
Because this number is bigger than 3/4, this is not the answer:

C)

Let's choose the points (2, -4) and (-2, 2), which are marked in the graph. WIth them, we calculate the following:

`a_C=(2-(-4))/(-2-2)=(6)/(-4)=-(3)/(2)`

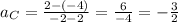
From this, we calculate the absolute value, which is 3/2 (positive), which is bigger than 3/4, and for this reason, also not our correct answer.

D)

To calculate this one we will use the points (-6, -11) and (-2, -5), which will allow us to perform the following calculation: