The free body diagram for block 2 is:
(Notice how we establsh the postive x-direction to the left since we expect the block to move to the left)
Now for block 1 we have:
(Once again we establish the positive x-direction to the left)
The equations of motion for block 1 are:
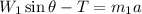
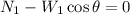
The equations for block 2 are:
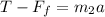
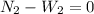
We know that the force of friction is equalt to the coefficient of friction multiplied by the normal force, then for the second block we have:

With this we have the following system for the unknowns:
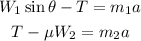
From the first equation we have that:
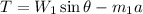
plugging this in the second equation we have:
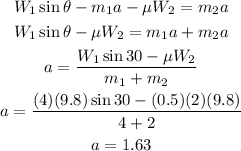
Therefore the acceleration is 1.63 meters per second per second. (Notice how it is positive, this means that the blocks move to the left as we expected)
Now we plug the value of the acceleration for the equation for the tension:
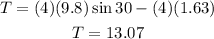
Therefore the tension is 13.07 N