We have to first find the compound function:
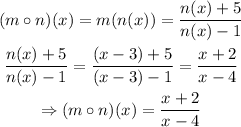
The domain of this compound function is all the real values but x=4, where the function has a discontinuity.
Then, any function that has a domain of "all real values but x=4" will have the same domain as our compound function.
This is the case for h(x)=11/(x-4), because it also has one discontinuity at x=4.
Answer: Third option, h(x)=11/(x-4)
![undefined]()