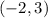We have the system
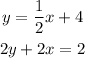
We solve it by substituting the value of y from the first equation into the second.
substituting = 1/2x+4 into 2y+2x=2 gives us
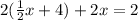
expanding the above LHS of the above gives
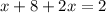
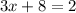
subtracting 8 from both sides gives
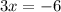
finally, dividing both sides by 3 results in
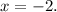
And we have the value of x. Now let us find y.
Substituting x = -2 into y= 1/2x+4 gives
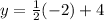
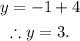
Thus we have the value of both x and y, and now we are in a position to write the solution to the system.
The solution to the system is