The diagram shows a triangle bisected by a perpendicular bisector RC. This means the angle PCQ has been divided into two equal halves which are;
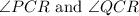
Note also that triangle PRC and triangle QRC both have the line segment RC in common.
Then if the line segment RC is a perpendicular bisector of line PQ, it means line segment PR equals RQ.
Therefore, in both triangles PRC and QRC, there is a congruence;
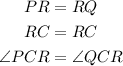
Hence, line PC equals line QC.
We can now et up the following equation.
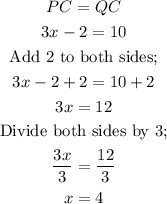
ANSWER;
x = 4
The correct answer is option C