Question

Hello pls do it and I will compare mine to your thanks person I don’t know

Answer 1

The given figure is compounded by a semicircle and a triangle as can be seen in the following diagram:

The area of a semicircle is given by the formula:

`A_(sc)=(\pi r^2)/(2)`

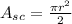
Where r is the radius of the semicircle, which is the half of the given diameter, then r=16/2=8 m. By replacing this value we can find the area of the first part:

`A_(sc)=(\pi(8m)^2)/(2)=(\pi\cdot64m^2)/(2)=100.5m^2`

Now, the area of the triangle is given by the formula:

`A_t=(b\cdot h)/(2)`

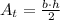
Where b is the base and h is the height. The base is b=16 m and h=12 m. Replace these values and find the area of this part:

`A_t=(16m\cdot12m)/(2)=(192m^2)/(2)=96m^2`

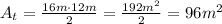
Finally, the total area of the figure is the addition of the two areas we found:

`A_{\text{fig}}=100.5m^2+96m^2=196.5m^2`

The answer is B. 196.5 m^2