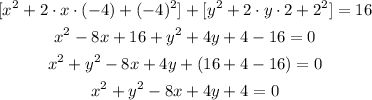The general equation of a circle is:

where (h, k) is the center and r is the radius.
From the graph, the center is located at (4, -2), that is, h = 4, and k = -2. And the radius is 4, that is, r = 4. Substituting into the general equation, we get:
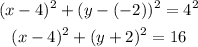
Solving the square of the binomials, and combining similar terms: