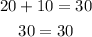Question

Need help don't know how to do this.

Answer 1

The equation for the total points is:

`100=(3)x+(4)y`

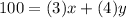
where x is the number of question that worth 3 points and y is the total pionts that worths 4 points. Now we know that in total we can have 30 questions so:

`x+y=30`

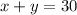
so now we have two incognitas and two equations so we can solve it. so in the secon ecuation we can solve for x so:

`x=30-y`

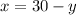
now we can substitude x in the first equation like this:

`100=3(30-y)+4y`

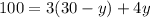
and we can solve for y

`\begin{gathered} 100=90-3y+4y \\ 100-90=4y-3y \\ 10=y \end{gathered}`

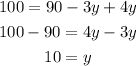
Now with the value of y we can replace that in the second equation to find x so

`\begin{gathered} x=30-y \\ x=30-10 \\ x=20 \end{gathered}`

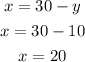
So there will be 20 3-points questions and 10 4-points questions

and we can prove it, replacing the values in the two equation so:

in the first equation:

`\begin{gathered} 100=(3)\cdot(20)+(4)\cdot(10) \\ 100=60+40 \\ 100=100 \end{gathered}`

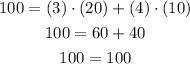
and in the secon equation:

`\begin{gathered} 20+10=30 \\ 30=30 \end{gathered}`