Question

There are 2 inequalities written below. Solve both inequalities, and justify your solution with a check step.a.b.2x < -4- 2x < 4What is the challenge with the inequality - 2x <4? Is it what you expected?

Answer 1

ANSWER and EXPLANATION

a. The first inequality given is:

`2x<-4`

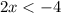
To solve this, divide both sides of the inequality by 2:

`\begin{gathered} (2x)/(2)<-(4)/(2) \\ x<-2 \end{gathered}`

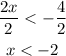
To justify this, pick any number less than -2 and substitute it back into the original inequality:

Let x be -4:

`\begin{gathered} 2(-4)<-4 \\ \Rightarrow-8<-4 \end{gathered}`

As we can see, it is correct.

b. The second inequality given is:

`-2x<4`

To solve this, divide both sides by -2. The sign changes from < to > because we are dividing both sides by a negative number.

Therefore:

`\begin{gathered} x>(4)/(-2) \\ x>-2 \end{gathered}`

To justify this, pick any number greater than -2 and substitute it back into the original inequality:

Let x be -1:

`\begin{gathered} -2(-1)<4 \\ 2<4 \end{gathered}`

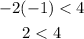
As we can see, it is correct.

The only challenge with solving the second inequality (-2x < 4) is that we have to change the sign form less than (<) to greater than (>) due to the division by a negative number.