Question

Since the balll is at a height of 0 feet at x=0 and x=70, then the maximum height is archieved at x=35.Use the function rule to determine that maximum height and confirm it on the graph.h(x) = -0.03x (x-70)

Answer 1

The maximum height refers to the vertical coordinate of the vertex V(h,k), where

`h=-(b)/(2a)`

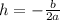
According to the given equation, we have the following

`h(x)=-0.03x(x-70)=-0.03x^2+2.1x`

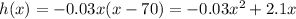
Where a = -0.03 and b = 2.1

`h=-(2.1)/(2\cdot(-0.03))=(2.1)/(0.06)=35`

Then, we find k by evaluating the function when x = 35.

`h(35)=-0.03\cdot35(35-70)=-1.05(-35)=36.75`

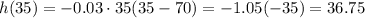
Hence, the maximum height is 36.75 feet.