We have that probability is the number of successes of an event under the number or possible cases.
We have a spinner with 15 equal-size number sections. Therefore, there are the following possibilities:
1, 2, 3 ,4, 5 ,6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
The multiples of 3 (in this list of numbers) are:
3 * 1 = 3
3 * 2 = 6
3 * 3 = 9
3 * 4 = 12
3 * 5 = 15
The multiples of 5 are:
5 * 1 = 5
5 * 2 = 10
5 * 3 = 15
Therefore, we have:
There are 5 cases in which they are multiples of 3. Then, we have:
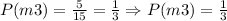
On the other hand, we have 3 cases in which they are multiples of 5. Thus:

Therefore, the probability that the number you spin is a multiple of 5 or multiple of 3 is the sum of both probabilities:
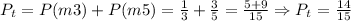
Therefore, the probability for this event is equal to 14/15.