Question

Real life application: A line is represented by the equation ax+ by =4 a. When is the line parallel to the x-axis? b. When is the line parallel to the y-axis? c. Give values for a and b such that the line has a slope of 5/8

Answer 1

The equation of a line is given by,

`ax+by=4\text{ ---(1)}`

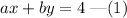
The general equation of a line is given by,

`y=mx+c\text{ ---(2)}`

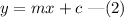
Here, m is the slope of the line and c is the y intercept.

Rewrite equation (1) into the form of equation (2).

`\begin{gathered} by=-ax+4 \\ y=(-a)/(b)x+(4)/(b)\text{ ---(3)} \end{gathered}`

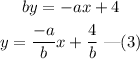
Comparing equations (2) and (3), the slope of the line is

m=-a/b and the y intercept c=4/b

a)

A line is parallel to the x axis when the slope is equal to zero.

Therefore, the given line is parallel to the x axis if,

`\begin{gathered} m=0 \\ (-a)/(b)=0 \\ a=0 \end{gathered}`

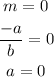
Since y intercept c=4/b , b cannot be zero.

So, the given line is parallel to the x axis when a=0 and b≠0.

b)

The line is parallel to the y axis when the slope is undefined.

When the line is parallel to the y axis, the x intercept can be found by putting y=0 in equation (1).

`x=(4)/(a)`

The given line is parallel to the y axis when b=0 and a≠0.

c)

Given, the slope of line is m= 5/8.

From equation (2), the slope of line is m=-a/b.

Therefore,

`\begin{gathered} (-a)/(b)=(5)/(8) \\ (a)/(b)=(-5)/(8) \end{gathered}`

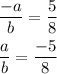
Therefore, we can take a=-5 and b=8 when the line has slope 5/8.