The distance KJ needs to be equal to the distance LM and KL need to be parallel to JM
distances
![d_(KJ)=\sqrt[]{(-2+4)^2+(-6+2)^{}^2}=2\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2ifn3yc5l05g0l9a6oxn4eo7tp2jgvp8hh.png)
![d_(LM)=\sqrt[]{(-1-4)^2+(2-2)^2}=5](https://img.qammunity.org/2023/formulas/mathematics/high-school/ddrb3uk9oo4qiv3mrwq07o4ubqw9okh3oy.png)
then we need to calculate the slope of LK and JM if they are equal we have parallel sides
for LK
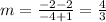
for JM
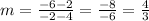
This figure is a trapezoid because it has exactly one pair of parallel sides that can prove because the slopes of LK and JM are congruent, but the distances KJ and LM are not equal therefore it is not an isosceles trapezoid