Graphing the points given and the corresponding sides, we have:
We can see that the distance between P and Q and the distance between R and S is 7 units (they have the same y-coordinate, so the distance is the difference in x-coordinates).
Also, the vertical distance between Q and R and the vertical distance between P and S is 9 units (just the difference in y-coordinates).
Since this figure is a parallelogram (opposite sides are parallel), we can calculate the area as the base PQ times the height (the height is 9 units):
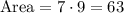
The length of segments QR and PS can be calculated using Pythagorean Theorem, with the difference in x-coordinates being 3 units and the difference in y-coordinates being 9 units:
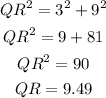
So the perimeter of this parallelogram is:
