the common difference d is 3
therefore, the first term is 17
Step-by-step explanation
an arithmetic serie is given by the expression
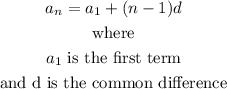
Also, the sum of the x terms of the serie is given by
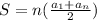
then
Step 1
set the equations
The 7th term of an arithmetic series is 35.
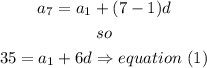
and, The sum to the 10th term of the series is 305,
let n= 10
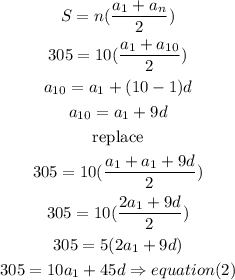
Step 2
solve the equations
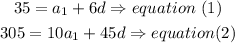
a) isolate the a1 value form equation(1) and replace in equation (2)
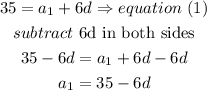
replace in eq(2)

therefore,
the common difference d is 3
b) now, replace the d value in equation(1) and solve for a1
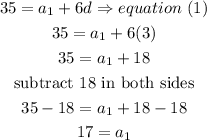
therefore, the first term is 17
I hope this helps you