Answer:
The company would save $10.5
Explanation:
First, we have to remember that the total surface area of a rectangular box is:
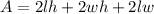
Where:
• l, is the ,lenght, of the box
,
• w, is the ,width, of the box
,
• h ,is the ,height, of the box
Now, let's calculate the total surface area of each one of the boxes:
BOX 1:
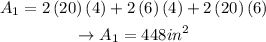
BOX 2:
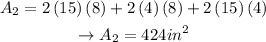
Now, let's convert each surface area into square foot:
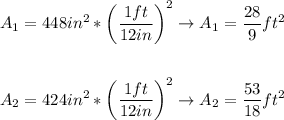
Now, we multiply each surface area by the cost of the material per square feet to find the cost of one unit of each box:
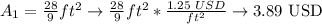
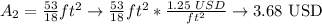
Now we multiply this individual cost by 50 to get the cost of 50 boxes of each type:
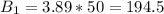
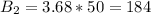
Now, we find the difference between both prices:
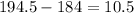
This way, we can conlcude that the company would save $10.5