A line equation can be written in slope-intercept form, whih is

where m represents the slope and b represents the y-intercept.
Since our line passes through the origin, we already know that b = 0. To find the slope of our line, we can evaluate any of the points that belongs to our line on the slope-intercept form then solve it for m. The point (12, 200) for example belongs to our line. Evaluating this point on the form, we have:
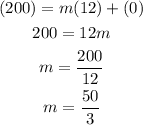
therefore, our line equation is
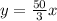
The correct answer is option A.