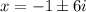Given the quadratic equation
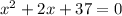
We can find the solution using the quadratic formula. The formula for the method is given below.
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
To get a,b,c we would compare the given equation with the general representation of a quadratic equation
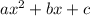
Therefore, a=1, b=2 and c=37
Thus;
![\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-(4*1*37)}}{2*1} \\ x=\frac{-2\pm\sqrt[]{4-148}}{2} \\ x=\frac{-2\pm\sqrt[]{-144}}{2} \\ \therefore i^2=-1 \\ We\text{ would have;} \\ x=\frac{-2\pm\sqrt[]{144i^2}}{2} \\ x=(-2\pm12i)/(2) \\ x=(2(-1\pm6i))/(2) \\ x=-1\pm6i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iwz2xj17j8sy9xd31am9sdnt0t2bgadfy6.png)
Answer: