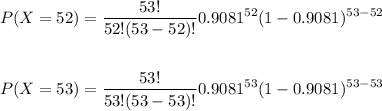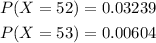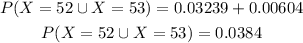Question

Suppose that the probability that a passenger will miss a flight is 0.0919. Airlines do not like flights with empty seats, but it is alsonot desirable to have overbooked flights because passengers must be "bumped" from the flight. Suppose that an airplane has aseating capacity of 51 passengers.(a) If 53 tickets are sold, what is the probability that 52 or 53 passengers show up for the flight resulting in an overbooked flight?(b) Suppose that 57 tickets are sold. What is the probability that a passenger will have to be "bumped"?(c) For a plane with seating capacity of 280 passengers, what is the largest number of tickets that can be sold to keep theprobability of a passenger being "bumped" below 1%?

Answer 1

Given

Passenger misses a flight 0.0919

Flying capacity 51 passengers

Definitions

Definition binomial probability

`P(X=k)=(n!)/(k!(n-k)!)p^k(1-p)^(n-k)`

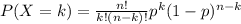
Addition rule for disjoint or mutually exclusive events

`P(\text{AUB)}=P(A)+P(B)`

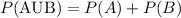
(a) if 53 tickets are sold

`n=53`

Evaluate the definition of binomial probability ar x = 52, 53

`\begin{gathered} P(X=52)=(53!)/(52!(53-52)!)0.9081^(52)(1-0.9081)^(53-52) \\ \\ P(X=53)=(53!)/(53!(53-53)!)0.9081^(53)(1-0.9081)^(53-53) \end{gathered}`
`\begin{gathered} P(X=52)=0.03239 \\ P(X=53)=0.00604 \end{gathered}`
`\begin{gathered} P(X=52\cup X=53)=0.03239+0.00604 \\ P(X=52\cup X=53)=0.0384 \end{gathered}`