1 Answer

Newaj · Answer 1 · 2023-11-01T04:06:52+0000

The given figure is formed by a cylinder and a cone.

The volume of a cone is

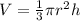
$V=(1)/(3)\pi r^2h$

Where pi = 3.14, r = 5 cm, and h = 13 cm. Let's replace these values

$\begin{gathered} V=(1)/(3)\cdot3.14\cdot(5cm)^2\cdot13\operatorname{cm} \\ V=340.17\operatorname{cm}^3 \end{gathered}$

The volume of a cylinder is

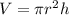
$V=\pi r^2h$

Where pi = 3.14, r = 5cm, and h = 2 cm. Let's replace these values

$\begin{gathered} V=3.14\cdot(5cm)^2\cdot(2\operatorname{cm})=3.14\cdot25\cdot2 \\ V=157\operatorname{cm}^3 \end{gathered}$

Then, we add both volumes to find the total

$V_{\text{total}}=340.17+157=497.17\operatorname{cm}^3$

Please log in or register to add a comment.