Given: Two pictures (P1 and P2) with dimensions below:
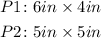
To determine: If the same amount of framing is needed for each pictures
In other to achieve this, we would assume that the outside dimension of the pictures were given and let the moulding of the frames (F1 and F2) be 1 inches wide.
Calculate the area of the outside dimension of the Pictures
The shape of the picture is a rectangle. The area of a rectangle is given by the formula:
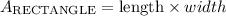
Therefore, the area of the pictures would be
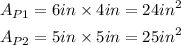
Calculate the dimensions of the two frames
We assume the moulding or the edges of the frame is 1 inches wide. Then the dimensions of the frames would be
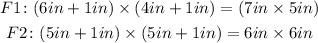
Calculate the area of the Frames:
The area of the frames would be area of a rectangle which is length times width
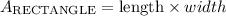
Therefore, the area of the frames is as calculated below:
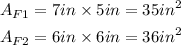
State the observation from the calculated area of frames
It can be observed from the calculations above that the areas of the pictures and the frames are not the same. Therefore, we can conclude that:
Mr Forster does not need the same amount of framing for each picture