Question

Caroline is considering two video game rental plans. Plan A can be modeled with the equation C = 2n, and Plan B can be modeled with the equation C = n + 6, where C represents the cost in dollars and n represents the number of games rented each month. Which statement would justify selecting Plan A instead of selecting Plan B?

Answer 1

To justify selecting Plan A instead of selecting Plan B, we need to compare their cost equations. Plan A has a lower cost for each game rented compared to Plan B.

Step-by-step explanation:

To justify selecting Plan A instead of selecting Plan B, we need to compare their cost equations. Plan A is modeled by the equation C = 2n, where C represents the cost and n represents the number of games rented. Plan B is modeled by the equation C = n + 6. Comparing the two equations, we can see that Plan A has a lower cost for each game rented compared to Plan B. For example, if you rent 5 games, Plan A would cost $10 (2 * 5) while Plan B would cost $11 (5 + 6).

Therefore, Plan A would be the better choice if you want to save money on each game rented.

Answer 2

Options

A. Caroline rents exactly 7 games each month.

B. Caroline rents exactly 6 games each month.

C. Caroline rents 6 or more games each month.

D. Caroline rents from 1 to 5 games each month.

Answer:

D. Caroline rents from 1 to 5 games each month.

Step-by-step explanation:

Given

Plan A:

`C = 2n`

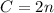
Plan B:

`C = n + 6`

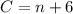
Required

Which options justifies A over B

The solution to this question is option (d).

In option d, n = 1,2,3,4,5

When any of the values of n is substituted in plan A and B, respectively; the cost of plan A is cheaper than plan B.

This is not so, for other options (A - C)

To show:

Substitute 1 for n in A and B

Plan A:

`C = 2n`
`= 2 * 1 = 2`

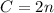
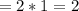
Plan B:

`C = n + 6`
`= 1 + 6 = 7`

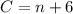
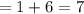
Substitute 5 for n in A and B

Plan A:

`C = 2n`
`= 2 * 5 = 10`

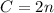
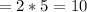
Plan B:

`C = n + 6`
`= 5 + 6 = 11`

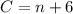
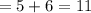
See that A < B