Options
A. Caroline rents exactly 7 games each month.
B. Caroline rents exactly 6 games each month.
C. Caroline rents 6 or more games each month.
D. Caroline rents from 1 to 5 games each month.
Answer:
D. Caroline rents from 1 to 5 games each month.
Step-by-step explanation:
Given
Plan A:

Plan B:
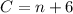
Required
Which options justifies A over B
The solution to this question is option (d).
In option d, n = 1,2,3,4,5
When any of the values of n is substituted in plan A and B, respectively; the cost of plan A is cheaper than plan B.
This is not so, for other options (A - C)
To show:
Substitute 1 for n in A and B
Plan A:

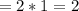
Plan B:
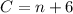
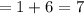
Substitute 5 for n in A and B
Plan A:

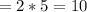
Plan B:
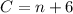
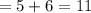
See that A < B