Question

Find the coordinates of the point of intersection of the diagonals of parallelogram ABCD with the vertices:A(-1,3), B (3,3), C (5, -1), and D (1, -1)

Answer 1

Part 1

We have the following points given:

A (-1,3) B(3,3) C(5, -1) and D(1, -1)

The diagonals for this case are:

AC and BD

Then we can find the midpoint with the following points:

A (-1,3) C(5,-1)

`x=(x_1+x_2)/(2)=(-1+5)/(2)=2`
`y=(y_1+y_2)/(2)=(3-1)/(2)=1`

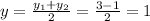
Then the midpoint would be:

(2,1)

Part 2

For this case we have the following points:

P(-3,2) Q(2,6) R(3,3) S(x,y)

We need to satisfy the following:

slope PS= slope QR

And replacing we got:

`(y-2)/(x+3)=(3-6)/(3-2)`

Solving we have the following equation:

(y-2) = (x+3)*-3

y -2= -3x-9

y= -3x -7

Then we can create this other equation:

slope PQ = slope RS

replacing we got:

`(y-3)/(x-3)=(6-2)/(2+3)`

Solving we got:

5(y-3) = 4(x-3)

5y-15 =4x-12

5y -4x = 3

Replacing the first equation we got:

5(-3x-7) -4x= 3

-15x -35 -4x = 3

-19 x= 38

x= -2

y= -3*(-2)-7= 6-7 =-1

Then the answer is:

S= (-2,-1)

Part 3

We have the following points:

A= (-3,4)

B= (3,2)

C=(2,-1)

D=(-4,1)

We can find the distance between points like this:

`d_(AB)=\sqrt[]{(3+3)^2+(2-4)^2}=\sqrt[]{40}`
`d_(BC)=\sqrt[]{(2-3)^2+(-1-2)^2}=\sqrt[]{10}`
`d_(CD)=\sqrt[]{(-4-2)^2+(1+1)^2}=\sqrt[]{40}`
`d_(DA)=\sqrt[]{(-4+3)^2+(1-4)^2}=\sqrt[]{10}`

Then AB= DA and BC= CD

Then the answer is:

Parallelogram

Rectangle