Question

Diane is walking. The number of minutes she has walked varies directly with the number of calories she has burned. See the graph below.

Answer 1

(a) How many calories is Henry burning per minute?

calorie(s)

4 calories

(b) What is the slope of the graph?

1/4

Explanation:

Answer 2

Explanation

We are given a graph that shows the relationship between the number of minutes and the calories burned

From the graph, we can infer that

When Diane burns 100 calories when she walks for 10 minutes

When she walks for 30 minutes, she will have burned 300 calories.

Therefore, to answer the first part of the question

Part A

if she burns 100 calories in 10 minutes

then in 1 minute, she burns

`(100)/(10)=10\text{ calories}`

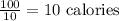
Therefore, every minute, Diane burns 10 calories

But the question wants us to get the number of minutes per calorie.

This will be obtained as follow:

`\begin{gathered} 100\text{ calories in 10 minutes} \\ Then\text{ 1 calorie will be burned in} \\ (10)/(100)=0.1\text{ minute} \end{gathered}`

Therefore, the answer to part A is 0.1 minute

Part B

The question wants us to get the slope of the line

The slope will be obtained by obtaining the change in the number of minutes walks to the number of calories burned, which is obtained from the graph above

`(y_2-y_1)/(x_2-x_1)=(30-10)/(300-100)=(20)/(200)=0.1`

Therefore, the slope is 0.1 minutes per calories