Question

(this is a 3 part question)The pilot of a plan points his airplane due South and flies with an airspeed of 120 m/s. Simultaneously, there is a steady wind blowing due West with a constant speed of 40 m/s. a. Make a sketch that shows how to find the resultant velocity of the the plane. Roughly in what direction is the resultant velocity?b. what is the resultant speed of the airplane?c. After one hour, how far away is the plane from it's starting point?

Answer 1

We are told that the pilot of a plane points his airplane due South and flies with an airspeed of 120 m/s. Simultaneously, there is a steady wind blowing due West with a constant speed of 40 m/s.

a. This can be represented in a diagram by;

To get the direction, consider the right-angled triangle seen in the diagram, with Opposite side of 40 units and Adjacent side of 120 units.

`\begin{gathered} \tan \text{ }\theta\text{ = }\frac{Opposite}{\text{Adjacent}}\text{ = }(40)/(120)\text{ = 0.3333} \\ \\ \theta\text{ = }\tan ^(-1)(0.3333)=18.43^0 \end{gathered}`

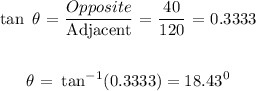
The direction of the resultant velocity is South 18.43 degrees West

To get the resultant speed, we make use of the concp;