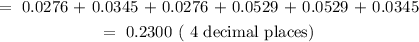SOLUTION:
Step 1:
In this question, we are given the following:
Step 2:
We have the following probabilities based on their colors:

a) Compute the probability that the randomly selected peanut M&M is not
orange:
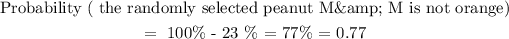
Step 3:
b) Compute the probability that the randomly selected peanut M&M is red or yellow:
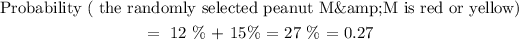
Step 4:
c) Compute the probability that the randomly selected peanut M&M are both green

Step 5:
d) If you randomly select two peanuts M&M's, compute the probability that neither of them are orange
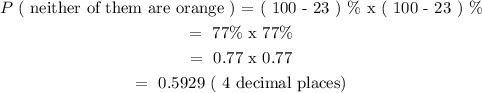
Step 6:
e) If you randomly select two peanut M&M's, compute that probability that at least is orange:
In this case, we would consider six different options here:
i ) Probability ( Brown & Orange )
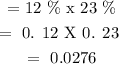
ii ) Probability ( Yellow & Orange):
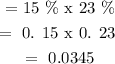
iii )Probability ( Red & Orange):
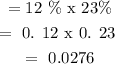
iv) Probability ( Blue & Orange ):
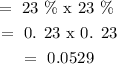
v) Probability ( Orange & Orange):
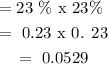
vi ) Probability ( Green & Orange):
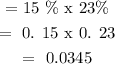
Now, we need to sum up the individual probabilities, we have that: