Question

HELP! 15 POINTS NO EXPLANATION NEEDED ANY WRONG ANSWERS ARE REPORTED PLEASE HELP

Answer 1

If we perform sintetic division on the polynomiapl P(x), assuming that x = -2 is a root, then we have:

notice that the last number on the final row is 0, this means that by the factor theorem, since the residue is 0, we have that (x+2) is a factor of the polynomial P(x). Also, we can evaluate -2 on P(x) to get:

`\begin{gathered} P(-2)=2(-2)^3+2(-2)^2-3(-2)+2 \\ =2(-8)+2(4)+6+2=-16+8+6+2=-16+16=0 \\ \Rightarrow P(-2)=0 \end{gathered}`

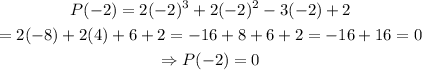
so, P(-2) = 0