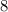Question

Help with this..but not Pauline helms she is unhelpful tutor.

Answer 1

Since the tangent of B is 4/3, then:

`\begin{gathered} (AC)/(BA)=(4)/(3) \\ \Rightarrow AC=(4)/(3)BA \end{gathered}`

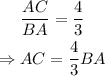
On the other hand, since ABC is a right triangle with hypotenuse BC, then:

`(BA)^2+(AC)^2=(BC)^2`

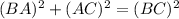
Substitute AC=3/4 BA and BC=15 to find BA:

`\begin{gathered} (BA)^2+((4)/(3)BA)^2=15^2 \\ \Rightarrow BA^2+(16)/(9)BA^2=15^2 \\ \Rightarrow(1+(16)/(9))BA^2=15^2 \\ \Rightarrow(25)/(9)BA^2=15^2 \\ \Rightarrow BA^2=(9)/(25)\cdot15^2 \\ \Rightarrow BA=\sqrt[]{((9)/(25)\cdot15^2)} \\ \Rightarrow BA=(3)/(5)\cdot15 \\ \Rightarrow BA=9 \end{gathered}`

Substitute BA=12 into the expression for AC to find its value:

`AC=(4)/(3)BA=(4)/(3)(9)=12`

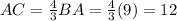
On the other hand, we know that:

`BD+DA=BA`

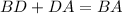
Substitute BA=12 and DA=3 to find BD:

`\begin{gathered} BD+3=9 \\ \Rightarrow BD=9-3 \\ \Rightarrow BD=6 \end{gathered}`

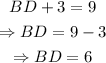
Finally, since BDE and BAC are similar triangles, we know that:

`\begin{gathered} (DE)/(BD)=(AC)/(BA) \\ \Rightarrow DE=(AC)/(BA)* BD \end{gathered}`

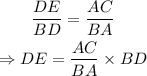
Substitute AC=12, BA=9 and BD=6 to find the length DE:

`\begin{gathered} DE=(12)/(9)*6 \\ \Rightarrow DE=8 \end{gathered}`

Therefore, the length of DE is:

`8`