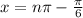Question

I need help with this practice problem, having a hard time solving it.It asks to graph the function, use desmos or your own paper. It is trig

Answer 1

Recall that the graph represented by the graph of h(x) translated horizontally n units to the left is:

`f(x+n)\text{.}`

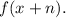
Therefore the graph of:

`f(x)=\cot (x+(\pi)/(6))`

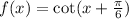
is the graph of

`h(x)=\cot (x)`

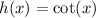
translated π/6 units to the left.

Now, recall that the asymptotes of h(x)=cot(x) are:

`x=n\pi\text{.}`

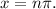
Then, the graph of h(x)=cot(x) is:

Therefore the graph of the given function is:

The asymptotes are of the form:

`x=n\pi-(\pi)/(6)`

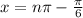
Answer:

The asymptotes are of the form:

`x=n\pi-(\pi)/(6)`