Question

Two manned satellites approaching one another at a relative speed of 0.300 m/s intend to dock. The first has a mass of 3.00 ✕ 103 kg, and the second a mass of 7.50 ✕ 103 kg. If the two satellites collide elastically rather than dock, what is their final relative velocity? Adopt the reference frame in which the second satellite is initially at rest and assume that the positive direction is directed from the second satellite towards the first satellite.

Answer 1

Given:

• Relative speed, v = 0.300 m/s

,

• Mass of satellite 1, m1 = 3.00 x 10³ J

,

• Mass of satellite 2, m2 = 7.50 x 10³ J

If both satellites collide elastically let's find their final relative velocity.

Apply the Law of Conservation of Momentum and Law of Conservation of Energy.

Since this is an elastic collision, the relative velocity of approach will always be equivalent to the relative velocity of separation.

We have:

`\begin{gathered} m_1u_1+m_2u_2=m_1v_1+m_2v_2 \\ \\ m_1u_1^2+m_2u_2^2=m_1v_1^2+m_2v_2^2 \end{gathered}`

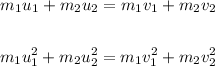
Now, divide both equations:

`u_1-u_2=-(v_1-v_2)`

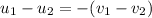
This means that the final relative velocity will also be equal to the initial relative velocity = 0.300 m/s.

• ANSWER: