Question

If you apply the changes below to the quadratic parent function, f(x) = x², which of these is the equation of the new function?• Shift 1 unit right.• Vertically stretch by a factor of 3.• Reflect over the x-axis.

Answer 1

If the parent quadratic function is shifted 1 unit right, we will subtract 1 on the "x" variable. The function becomes:

`g(x)=(x-1)^2`

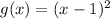
If the function is vertically stretched by a factor of 3, then the whole function is multiplied by 3. The function then becomes:

`g(x)=3(x-1)^2`

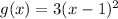
Then, lastly, to reflect the function over the x-axis, we will multiply the function by -1.

`g(x)=(-1)(3)(x-1)^2`

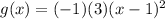
The function becomes:

`g(x)=-3(x-1)^2`

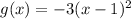
The equation of the new function after the given transformation is g(x) = -3(x - 1)² as shown above.