Question

What is the domain and range of the equation y = 6/(x+2) + 4?

Answer 1

The given equation is,

`y=(6)/(x+2)+4`

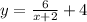
Domain function is defined everywhere except those values of argument

x when the denominator is zero.

That is,

x + 2 = 0

x = -2

SO the domain is,

`x\text{ }\\e-2`

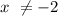
(Since x = -2 gives only 4)

domain is real numbers except -2.

putting, x = -2, we have,

`y=4`

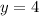
Therefore the range is

`y\\e4`

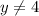
Thus range is real numbers except 4

Thus, correct option is (d)