We are given the following equation
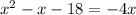
We are asked to solve for x by factoring the equation
Let us first simplify the equation
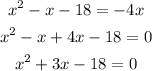
The equation has been simplified and now we can proceed to factor this equation
The standard form of a quadratic equation is given by
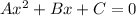
Comparing the standard form with our equation we see that
A = 1
B = 3
C = -18
Now to factor the equation, we need to think about two numbers such that
When we multiply them, we get A×C = -18
When we add them, we get B = 3
Can you think of such two numbers?
How about 6 and -3?
When we multiply them we get, 6×-3 = -18 (satisfied)
When we add them together we get, 6 +(-3) = 3 (satisfied)
So, our equation becomes
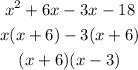
The above equation is the factorized equation.
Now let us solve for x
x + 6 = 0
x = -6
x - 3 = 0
x = 3
Therefore, the solutions of the given quadratic equation are x = (-6, 3)