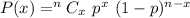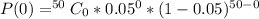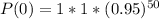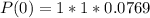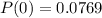Answer:
a.
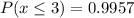 and
and
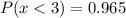
b.
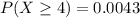
c.
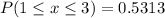
d.
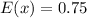 and
and
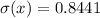
e.
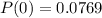
Explanation:
Given
X ~ Bin(15, 0.05)
This implies that:

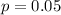
A binomial distribution is represented as:
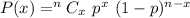
Solving (a):
(i)
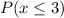
This is solved as:
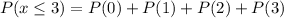
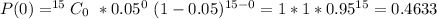
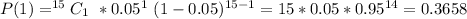
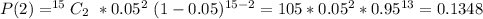
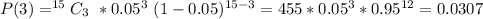
So:
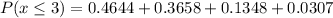
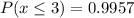
(ii)
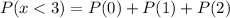
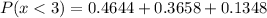
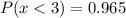
Solving (b):
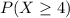
This is represented as:
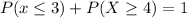
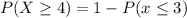
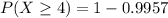
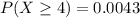
Solving (c):
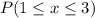
This is represented as:
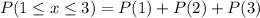
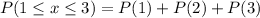
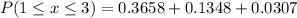
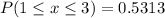
Solving (d): E(x) and Sigma(x)
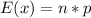
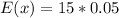
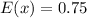
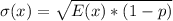
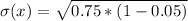
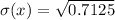
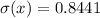
Solving (e):
Calculate P(0) when n= 50
Using: