Step-by-step explanation:
Taking into account the law of cosines, we can write the following equation:
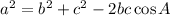
Then, replacing the values for a, b, and c, we get:
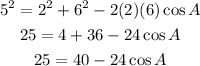
Solving for cos A, we get:

Therefore, the value of angle A is:
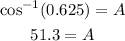
Now, we can use the law of sines, we can write the following equation:
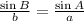
So, replacing the values and solving for B, we get:
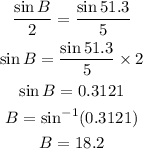
In the same way, Angle C is equal to:
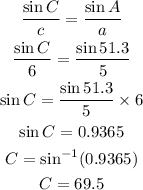
So, the answers are:
A = 51.3°
B = 18.2°
C = 69.5°