Question

I don't get it can someone help me.

Answer 1

EXPLANATION

Let's see the facts:

Length = 12+ 2*Width =12+2w

Width=w

Area= 14cm^2

The area of the rectangle is given by the following relationship:

`\text{Area}_{\text{rectangle}}=Length\cdot Width`

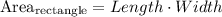
Replacing terms:

`14=(12+2\cdot\text{Width)}\cdot\text{Width}`

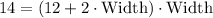
To make it more simple, let's call w to the width and apply the distributive property:

`14=12w+2w^2`

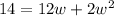
Subtracting -14 to both sides:

`0=2w^2+12w-14`

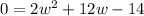
Applying the quadratic roots formula:

`w_1,w_2=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}`

We have a=2, b=12 and c=-14

Replacing terms:

`w_1,w_2=\frac{12\pm\sqrt[]{12^2-4\cdot2\cdot(-14)}}{2\cdot2}`

Multiplying numbers:

`w_1,w_2=\frac{12\pm\sqrt[]{144-112}}{4}`

Subtracting numbers:

`w_1,w_2=\frac{12\pm\sqrt[]{32}}{4}=\frac{12\pm4\sqrt[]{2}}{2}=6\pm2\sqrt[]{2}`

The solutions to the quadratic equation are:

`w_1=8.82,w_2=3.17`

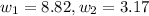
We have two possible solutions, w_1=8.82 cm and w_2=3.17 cm. Let's take w_2=3.17 cm as a solution:

The length would be as follows:

The answers are:

Width = 3.17 cm = 317/100 cm

Length = 18.34 cm = 917/50 cm