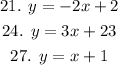Question

Write each equation in slope-intercept form.21. y -6 =-2(x + 2)24. y -8 = 3(x + 5)27.y-1/2=x+1/2

Answer 1

The slope-intercept form is given by

`y=mx+b_{}`

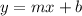
Where m is the slope, b is the y-intercept.

Let us convert the given equations into the slope-intercept form.

`y-6=-2\mleft(x+2\mright)`

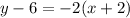
Expand the parenthesis on the right and then separate the y variable on the left side.

`\begin{gathered} y-6=-2x-4 \\ y=-2x-4+6 \\ y=-2x+2 \end{gathered}`

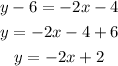
Similarly, repeat the above process for the 2nd equation

`\begin{gathered} y-8=3\mleft(x+5\mright) \\ y-8=3x+15_{} \\ y=3x+15+8_{} \\ y=3x+23 \end{gathered}`

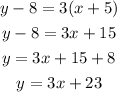
Finally, the 3rd equation

`\begin{gathered} y-(1)/(2)=x+(1)/(2) \\ y=x+(1)/(2)+(1)/(2) \\ y=x+1 \end{gathered}`

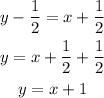
Therefore, the equations in the slope-intercept form are

`\begin{gathered} 21.\: \: y=-2x+2 \\ 24.\: \: y=3x+23 \\ 27.\: \: y=x+1 \end{gathered}`