Question

What is the molarity of a solution composed of 106 g Na Cozin 6.00 L ofsolution?

Answer 1

To solve this problem, we're going to use the formula of molarity:

`\text{Molarity (M)=}\frac{mole\text{s of solute}}{liter\text{s of solution}}\text{.}`

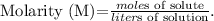
We have to find the number of moles in 106 g of Na. The molar mass of Na can be found in the periodic table, which is 23 g/mol. The conversion would be:

`106\text{ g Na}\cdot\frac{1\text{ mol Na}}{2\text{3 g Na}}=4.61\text{ moles Na.}`

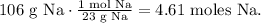
Finally, we replace the moles (4.61 moles) and the liters of solution (6.00 L) in the formula:

`\text{Molarity = }\frac{4.61\text{ moles}}{6.00\text{ L}}=0.768\text{ M.}`

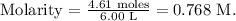
The molarity of the solution would be 0.768 M.